Before delving into the concept of Scales of Measurement, let’s first grasp the fundamental notion of ‘Measurement’.

Measurement is the process of assigning numerical values to individuals or their characteristics based on specific rules. L. R. Gay simplified it as quantifying the extent to which someone or something possesses a given trait.

For example, if a student gets 75 marks out of 100 on a test, it is measurement. The measurement represents the numerical result of the performance.

Scales of measurement categorize the numerical values assigned during measurement. In other words, scales of measurement refer to different ways or levels of categorizing and quantifying data. These scales help researchers and analysts understand the nature of the data they are working with and determine the appropriate statistical techniques to use for analysis.

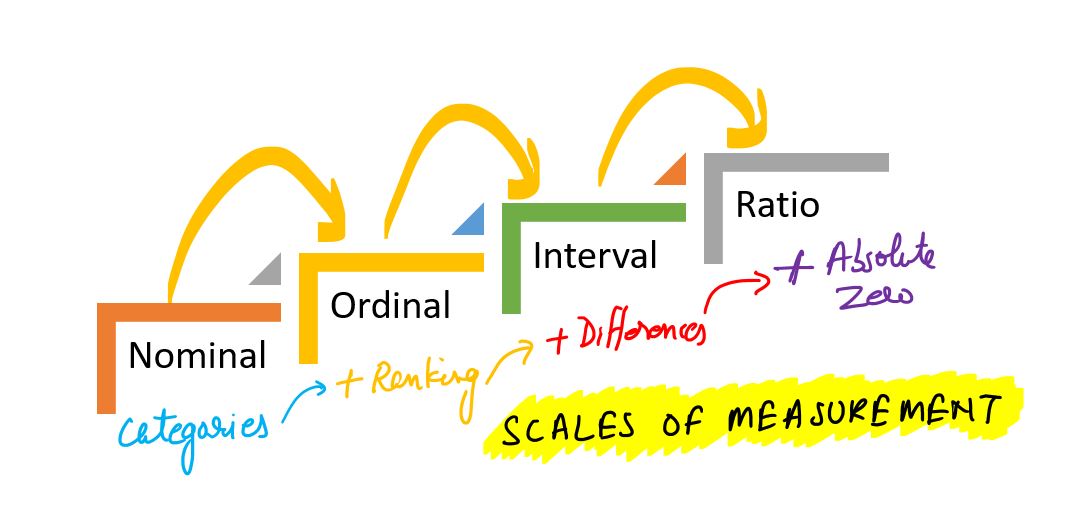
There are following 4 main scales of measurement. 

1. Nominal Scale

The nominal scale is the most basic form of measurement, dealing with non-numeric variables or numeric values with no inherent significance. It assigns categories to data without any particular order or structure.

An example of a nominal scale is the classification of colors; classification of population on the basis of gender etc. In research, a YES/NO scale is a nominal scale as it lacks any ordering or measurable distance between YES and NO.

2. Ordinal Scale

The ordinal scale permits the ranking of data (1st, 2nd, 3rd, etc.) based on their order, but it doesn’t quantify the differences between these ranks. It is suitable for situations where the order matters, but the extent of difference is not significant.

For instance, letter grades like A, B, C, and D represent an ordinal scale; while A is better than B, the scale doesn’t convey how much better it is. Order matters, but the differences between grades are not precisely quantified.

3. Interval Scale

Interval scales are numeric scales that not only establish an order but also provide consistent and meaningful differences between values.

An example of an interval scale is the Celsius temperature scale, where the difference between each degree is consistent (e.g., 60 to 50 degrees is a measurable 10 degrees, just as 80 to 70 degrees is). Time is another example of an interval scale with known, consistent, and measurable increments.

4. Ratio Scale

The ratio scale of measurement is the most informative one, encompassing the characteristics of the three earlier scales. Like a nominal scale, it assigns labels to objects. Like an ordinal scale, it orders these objects. Similar to an interval scale, it maintains consistent differences between units. Additionally, a ratio scale has an absolute zero point, indicating the complete absence of the measured quantity.

Examples of ratio variables include height and weight. Ratio scales permit meaningful arithmetic operations like addition, subtraction, multiplication, and division, and they support a wide range of descriptive and inferential statistical analyses.

UGC NET Previous Year Questions (Scales of Measurement)

1.) Which of the following type of variables would have a true zero point? (UGC NET 16 June 2023 Evening Paper)
(A) Nominal
(B) Ordinal
(C) Interval
(D) Ratio
ANS. D

2.) Given below are two statements: (UGC NET 13 June 2023 Evening Paper)
Statement I: In a ratio scale, zero point is arbitrary
Statement II: The nominal scale allows ordering/ranking of data
In the light of the above statements, choose the correct answer from the options given below
(A) Both Statement I and Statement II are true
(B) Both Statement I and Statement II are false
(C) Statement I is true but Statement II is false
(D) Statement I is false but Statement II is true
ANS. B

3.) Which of the following scales of measurement is synonymous to ranking or grading? (10 Oct 2022 Evening)
(A) Nominal scale
(B) Ordinal scale
(C) Interval Scale
(D) Ratio Scale
ANS. B

4.) Which of the following is considered as the highest scale in measurement? (29 Oct 2022 Evening)
(A) Nominal
(B) Ordinal
(C) Internal
(D) Ratio
ANS.